Mathematical model of the relationship between grinding process and residual stress on grinding surface

Abstract: Based on the analysis of the formation mechanism of residual stress on the grinding surface, a mathematical model reflecting the relationship between the grinding process and the residual stress of the grinding surface is established. The model reflects the law that the force, temperature and grinding fluid cooling performance affect the residual stress of the grinding surface during the grinding process.

1 Formation mechanism of residual stress on the surface of grinding

  1. Effect of plastic bulging effect

    2. During grinding, due to the large negative rake angle of the abrasive grain cutting edge, the plastic deformation of the deformation zone is very serious, and a complex stress state will be formed in the front region of the abrasive grain tip. On the surface portion where the abrasive cutting edge has just passed, plastic shrinkage occurs along the surface direction, and tensile plastic deformation occurs in the vertical direction of the surface - this is the plastic convex effect, and as a result, residual tensile stress occurs on the ground surface.
  2. Effect of light extrusion

    3. During the cutting process, a force is generated between the tool and the workpiece. The force perpendicular to the surface being machined and the resulting friction force together produce a squeezing effect on the surface being machined. When the blade is not sharp or the cutting conditions are bad, the effect of the squeezing effect is more obvious, and the squeezing effect causes residual compressive stress on the surface of the part.
  3. Thermal stress

    4. During grinding, the ground surface layer is thermally expanded by the heat of grinding, while the temperature of the substrate is low, and the thermal expansion of the ground surface layer is restricted by the substrate to generate compressive stress. When the temperature of the surface layer exceeds the temperature allowed by the elastic deformation of the material, the surface layer generates residual tensile stress when the temperature of the surface layer falls to coincide with the temperature of the substrate.
  4. Grinding fluid cooling effect

    5. During the grinding process, due to the use of the grinding fluid, the grinding surface layer will produce a cooling gradient during the cooling process, which is opposite to the influence of the thermal stress, which can alleviate the surface residual tensile stress caused by the thermal stress.
    In the grinding process, in addition to the above factors affecting residual stress, there are secondary quenching of the surface layer and tempering of the surface layer.

2 Establishment of mathematical model for grinding surface residual stress


According to the above analysis, the main factors affecting the residual stress of the grinding surface can be summarized as: grinding force, grinding temperature and cooling of the grinding fluid. The force and temperature are two kinds of grinding phenomena generated during the grinding process, which directly affect the residual stress. The influence of the grinding fluid on the residual stress is directly generated by the surface cooling process on the one hand, and The effects on force and temperature are indirectly generated. This paper attempts to give a mathematical model reflecting the relationship between force, temperature and the cooling performance of the grinding fluid and the surface residual stress by the experimental data of force and temperature and the mathematical processing of the two-dimensional residual stress test data of the grinding surface. The mathematical model should include the above factors affecting the residual stress on the ground surface, ie
s RT = s F + s R + s L
Where: s RT - grinding surface residual stress
s F - the influence of grinding force

s R - the effect of grinding temperature

s L - the effect of the cooling performance of the grinding fluid
  1. Mathematical model of relationship between grinding force and residual stress

    2. First, the relationship between residual stress and plastic deformation is analyzed according to the model shown in Fig. 1. Fig. 1a shows two springs in a free state, and Fig. 1b shows a state in which two springs are placed between rigid plates. According to the equilibrium conditions
    N=k 1 k 2 (l 1 -l 2 )/(k 1 +k 2 )
    Where: N - the internal force of the spring after the two springs are placed in the rigid plate
    l 1 , l 2 - the length of the two springs in the free state
    k 1 , k 2 - the spring constant of the two springs
    l 1 -l 2 can be regarded as plastic deformation in the sense of this paper. It can be concluded from the above formula that the internal force is proportional to the plastic deformation, that is, the residual stress is proportional to the plastic deformation.

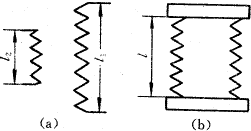    Fig.1 Relationship between residual stress and plastic deformation

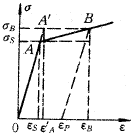    Figure 2 Simplified model of stress s and strain relationship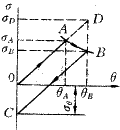
    image 3

    Figure 2 is a simplified model of the relationship between stress s and strain e . As can be seen from the figure
    e B =( s B - s S )/E 1 + e S &bnsp;&bnsp;&bnsp;&bnsp;&bnsp; e ' A = e B /E
    Where: s S - the yield limit of the material
    s B - the stress under a certain grinding condition
    E——the modulus of elasticity of the material
    E 1 ——Constant According to Fig. 2, when the external force is released, the strain e B at point B is released as e p after being released along the slope OA.
    e p = e B - e ' A =( s B - s S )/E+ e S + s B /E
    The above formula shows that plastic deformation is linear with force.
    Based on the above analysis, it can be recognized that the residual stress is linear with the grinding force, and the relationship between the two can be expressed as
    s F =AF+D 1 (1)
    Where: A, D 1 - coefficient
    F——grinding force (tangential force can be used)
  2. Mathematical model of relationship between grinding temperature and residual stress

    3. The residual stress generated by thermal stress can be analyzed by Figure 3. When the temperature of the grinding zone increases, the surface layer is thermally expanded to generate a compressive stress s , which increases linearly with increasing temperature, and its value is approximately
    s = a 'E Dq
    Where: a ′——linear expansion coefficient
    E——the modulus of elasticity of the material
    Dq ——When the grinding temperature continues to rise to q A , the thermal stress reaches the yield limit of the material. If the temperature rises again ( q A → q B ), the surface layer will plastically deform and the thermal stress value will stay. The yield limit at different temperatures of the material. After the grinding is completed, the surface layer temperature drops, and the thermal stress decreases according to the original slope s B (along the BC curve) until it is consistent with the substrate temperature, at which time the surface generates residual tensile stress. Its value is
    s q = s D - s B s D = a ′ E q B

    If s B is considered to be linear with temperature, then the mathematical model for the relationship between grinding temperature and residual stress can be obtained.
    s q = a ′ E q B -B 0 q B +D 2 =B q +D 2 (2)
    Where B 0 , B, D 2 - coefficient
    q ——Maximum temperature in the grinding zone
  3. Mathematical model of relationship between grinding fluid cooling performance and residual stress on grinding surface

    4. The higher the temperature in the grinding zone and the larger the cooling coefficient of the grinding fluid, the greater the temperature difference of the lower surface layer and the more the residual stress caused by the thermal stress is reduced. The effect of the cooling fluid cooling performance on the surface residual stress is related to the surface temperature. Therefore, the mathematical model of the relationship between the grinding fluid and the residual stress of the ground surface is expressed as
    s L =C q a +D 3
    Where C, D 3 - coefficient
    a —— Grinding fluid cooling coefficient synthesis (1), (2), (3) can be derived from the mathematical model of the relationship between grinding process and grinding surface residual stress is as follows
    s RT =AF+B q +C q a +D
    In the formula, A, B, C, D - reflect the coefficient of grinding force, grinding temperature, grinding fluid cooling performance affecting the residual stress of the grinding surface

3 Regression calculation and analysis of mathematical models

  1. Regression calculation of mathematical model

    2. According to the mathematical model of the residual stress expressed by equation (4), the following normal equations can be obtained by the least squares method.
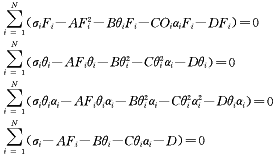
    In this paper, N=6, Table 1 is a calculation table of a set of measured data (residual stress unit is: MPa, the same below). Solving the normal equations
    A=45.77 B=1.98 C=-6×10 -4 D=-1.47

    The result of the fitting is as follows
    s RT =45.77F+1.98 q —6×10 -4 q a —1.47
    Table 1 Regression calculation table
    Specimen F i q i s i q 2 i F 2 i F i q i q i F i a i q 2 i a i q 2 i a 2 i s i F i s i q i s i q i a i q i a i
    1 1.84 280 421.4 78400 3.39 515.2 620300.8 9.44×10 7 1.14×10 11 775.38 117992 14.21×10 7 337120
    2 1.36 240 509.6 57600 1.82 326.4 56532.5 9.92×10 7 1.71×10 9 693.06 122304 21.17×10 6 41568
    3 1.70 212 441 44944 2.89 360.4 158559.1 2.1×10 7 9.83×10 9 749.7 93492 43.71×10 6 99152.4
    4 1.42 200 382.2 40000 2.02 284 229898 3.24×10 7 2.62×10 10 542.72 76440 61.84×10 6 161900
    5 1.62 260 460.6 67600 2.64 421.2 340961 5.47×10 7 4.43×10 10 746.17 119756 96.92×10 6 210470
    6 1.66 260 460.6 67600 2.77 431.6 349380 5.47×10 7 4.43×10 10 764.6 119756 96.92×10 6 210470
    s 9.6 1452 2675.4 356144 15.53 2338.8 1755631.4 26.71×10 7 24.03×10 10 435.88 649740 462.66×10 6 1.06×10 6

    Table 2 Error Analysis Table
    Specimen s  i s i D i D i / s * i (%)
    1 434.53 421.4 13.13 3.0
    2 510.87 509.6 1.27 0.2
    3 436.39 441 4.61 1.1
    4 362.21 382.2 19.99 5.5
    5 460.89 460.6 0.29 0.1
    6 462.66 460.6 2.06 0.5
  2. Analysis of mathematical model calculation results

    3. Table 2 is an error analysis table of the calculation results. Where s * i is the calculated value, s i is the measured value, D i =| s * i - s i |. The maximum fitting error is 5.5%.

4 Conclusion



This paper proposes a new method to study the residual stress of grinding surface, which is to study the residual stress of grinding surface with three comprehensive indexes reflecting the force, temperature and grinding fluid cooling coefficient of the grinding process. mathematical model. This mathematical model reflects the formation mechanism of residual surface stress on the ground surface, which is widely comparable to other single factor research methods.

Stainless Steel Precision Turned Parts

Precision turning parts

Precise accessory is a kind of high-precision hardware turning part processed by lathe and other machine tools, which is characterized by high precision, precision and small size

It is a very common product in our hardware processing parts industry and is widely used. The basic precision can reach 0.01mm-0.1mm. The products include steel, aluminum alloy, brass, environment-friendly iron, stainless steel and other precision CNC machining lathe parts of different sizes and shapes

Advantages of precision turning parts:

High technical requirements, beautiful appearance and good product quality

Scope of application:

Mechanical equipment, computers, mobile phones, electrical appliances, fans, cameras, high-end electronics, toys, instruments, automobiles, new energy, optical fiber communications, photographic stage equipment and other products.

Stainless Steel Precision Turned Parts,Cnc Turned Components,Turned Components,Cnc Precision Turning Parts

Stand Dragon Industrial Co., Ltd. , https://www.standdragontw.com